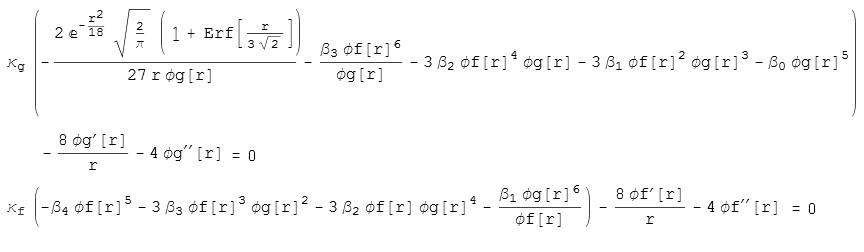Adding the second metric to the GR dust solution introduces a system of coupled ODE governing two conformal factors of two metrics.
In such a case, the ODE for the initial data becomes:
Here we demanded that the matter distribution profile is the same as in GR case. This is a generalized
Lane-Emden equation. In GR, the Lane-Emden equation occurs in the case of a polytropic fluid (which is a special case in the above equation for a fixed beta model). Hence, adding a second metric makes a pressureless fluid in one sector to appear as the influence of a nontrivial polytropic fluid on both metrics.
An example of the initial conditions is given in Figure 4.
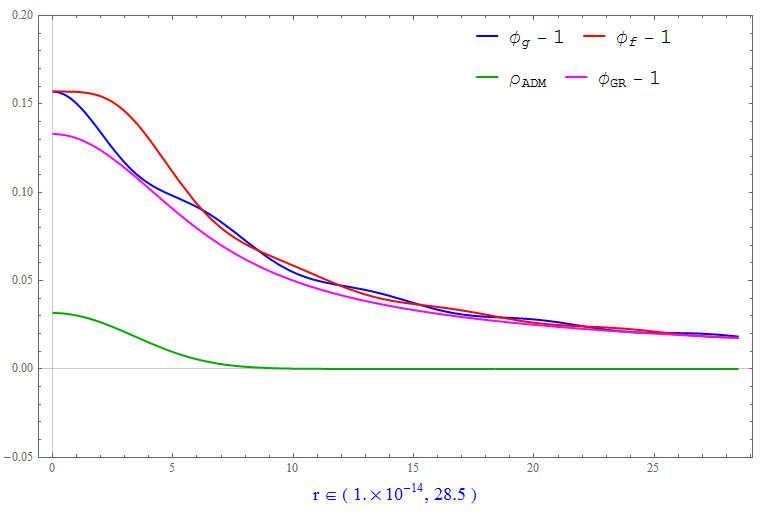
Figure 4.
In Figure 4, the testbed GR initial conditions are shown in magenta for comparison. The bimetric initial conditions are depicted in blue/red and appear as a wavy departure from GR. The evolution is under development :)
Figure 5.