| Tutorial #1 [] | Handout Solutions |
|
Notation, Lorentz invariance, Index gymnastics, Dirac delta function.
| |
| Tutorial #2 [] | Handout Notes Solutions |
|
Natural Units and Dimensional Analysis. SR recap II.
Ladder operators and Heisenberg algebra.
| |
| Tutorial #3 [] | Handout Fields overview Solutions |
|
Fourier Transform. The Lagrangian of the real scalar (KGF) field.
| |
| Tutorial #4 [] | Notes |
|
Group theory. Invariance in form and value.
Rotations in Euclidean 3D space and the deffnition of a group.
The Lorentz group.
The unitary group.
The generators of a group of differentiable transformations.
| |
| Tutorial #5 [] | Handout Part 1 Part 2 |
|
Part I. The quantization procedure.
The inverse operator expansion. The evaluation of the commutator [a,a†]. The evaluation of the equal time commutator for the fields.
| |
| Tutorial #6 [] | Handout Solutions Overview |
|
Part II. The expansion of the Hamiltonian. An introduction to the infinite contributions to
the energy and the normal ordering of operators.
(Additional references: Casimir effect.) Symmetries and Conservation Laws. Noether’s theorem. (Additional references: Chapter 8 from Hagen Kleinert's Book on Particles and Quantum Fields) | |
| Tutorial #7 [] | Handout I & II Solutions Notes |
|
The Dirac field, Part I. Gamma matrices (Dirac equation), Dirac algebra.
Part II.
Lorentz invariance of the Dirac equation. The Dirac equation for a free particle.
Properties of the energy projection operator. Additional problems.
| |
| Tutorial #8 [] | Solutions |
|
Dirac field and gamma matrices (contd). Maxwell field, gauge fixing. Highlights from Problem Set 1. | |
| Tutorial #9 [] | Handout Solutions |
|
The Schrödinger, Heisenberg and Interaction Pictures.
Perturbation Expansion of the S-Matrix.
Wick’s Theorem.
QED processes at 2nd order.
(Additional references:
The Schrodinger, Heisenberg and Interaction Pictures in QFT,
Invariant commutation and propagation functions)
| |
| Tutorial #10 [] | Solutions, Feynman diagrams |
|
Problems 7.1, 7.3 and 7.5 (Mandl & Shaw), Feynman amplitudes for QED.
| |
| Tutorial #11 [] | Handout Solutions |
|
Cross-sections.
The relativistic definition of flux.
The spin-sums lemma. The e-e+ production in electromagnetic field.
| |
| Tutorial #12 [] | Handout Solutions |
|
gamma^5 matrix and Left/Right-chiral fields.
Weyl fields (and problem of coupling by mass).
Transformation properties of vectors/axial vectors.
| |
| Tutorial #13 [] | Solutions |
|
Massive vector bosons (the Proca equation).
Propagating degrees of freedom for spin-1 fields.
EoM for the Yang-Mills Lagrangian.
SU(2) charges of weak interactions.
| |
| Tutorial #14 [] | Handout Solutions |
|
Higgs mechanism: generation of mass for Z bosons and photons, Higgs decays Suggested reading: Schwartz ch 29.1-29.2, Mandl and Shaw chapter 18-19 Additional notes on spontaneous symmetry breaking | |
| Tutorial #15 [] | Solutions |
|
Path Integrals. Preliminaries. Gaussian integrals. Grassmann numbers | |
| Tutorial #16 [] | Solutions |
|
Path Integrals, Part II. Perturbation expansion for the phi^4-theory.
| |
| Tutorial #17 [] | |
|
Old exam problems.
| |
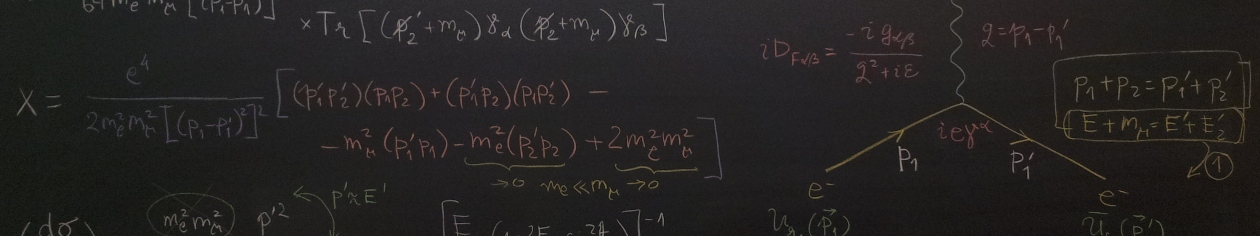
Quantum Field Theory
Course FK8027 HT19 / VT20
Tutorial Notes Homepage
Course FK8027 HT19 / VT20
Tutorial Notes Homepage